Chapter 30
2D Triangulation Data Structure

Table of Contents

30.1   Definition

30.1.1   A Data Structure Based on Faces and Vertices

The representation of CGAL 2D triangulations is based on faces and vertices, Edges are only implicitly represented trough the adjacency relations between two faces.

The triangulation data structure can be seen as a container for faces and vertices maintaining incidence and adjacency relations among them.

Each triangular face gives access to its three incident vertices and to its three adjacent faces. Each vertex gives access to one of its incident faces and through that face to the circular list of its incident faces.

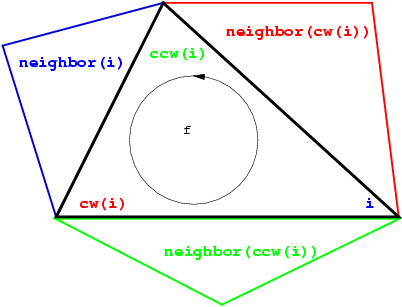
The three vertices of a face are indexed with 0, 1 and 2. The neighbors of a face are also indexed with 0,1,2 in such a way that the neighbor indexed by i is opposite to the vertex with the same index. See Figure 30.1, the functions ccw(i) and cw(i) shown on this figure compute respectively $$i+1 and $$i-1 modulo 3

Each edge has two implicit representations: the edge of a face f which is opposed to the vertex indexed i, can be represented as well as an edge of the neighbor(i) of f.

Figure 30.1:  Vertices and neighbors.

This kind or representation of simplicial complexes extends in any dimension. More precisely, in dimension $$d, the data structure will explicitly represents cells (i. e. faces of maximal dimension) and vertices (i. e. faces of dimension 0). All faces of dimension between $$1 and $$d-1 will have an implicit representation. The 2D triangulation data structure can represent simplicial complexes of dimension 2, 1 or 0.

30.1.2   The Set of Faces and Vertices

This rules extends to lower dimensional triangulation data structure arising in degenerate cases or when the triangulations have less than three vertices. A one dimensional triangulation structure maintains a set of vertices and edges which forms a ring topologically equivalent to a $$1-sphere.

A zero dimensional triangulation data structure only includes two adjacent vertices that is topologically equivalent to a $$0-sphere.

30.2   The Concept of Triangulation Data Structure

The triangulation data structure is required to provide:

• the types Vertex and Face for the vertices and faces of the triangulations
• the type Vertex_handle and Face_handle which are models of the concept Handle and through which the vertices and faces are accessed.
• iterators to visit all the vertices, edges and faces of the triangulation,
• circulators to visit all the vertices, edges and faces incident to a given vertex

The triangulation data structure is responsible for the creation and removal of faces and vertices (memory management). It provides function that gives the number of faces, edges and vertices of the triangulation.

The triangulation data structure provides member functions to perform the following combinatorial transformation of the triangulation:

• flip of two adjacent faces,
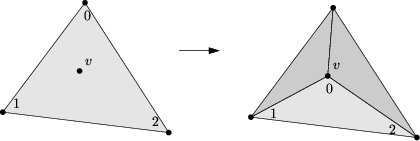
• addition of a new vertex splitting a given face see Figure 30.2,
• addition of a new vertex splitting a given edge,
• addition of a new vertex raising by one the dimension of a degenerate - lower dimensional triangulation,
• removal of a vertex incident to three faces,
• removal of a vertex lowering the dimension of the triangulation

Figure 30.2:  Insertion of a new vertex, splitting a face

30.3   The Default Triangulation Data Structure

CGAL provides the class CGAL::Triangulation_data_structure_2<Vb,Fb> as a default triangulation data structure.

30.3.1   Flexibility

This design allows the user to plug in the triangulation data structure his own vertex or face classes tuned for his application.

30.3.2   The Cyclic Dependency of Template Parameters

Figure 30.3:  The cyclic dependency in triangulations software design.

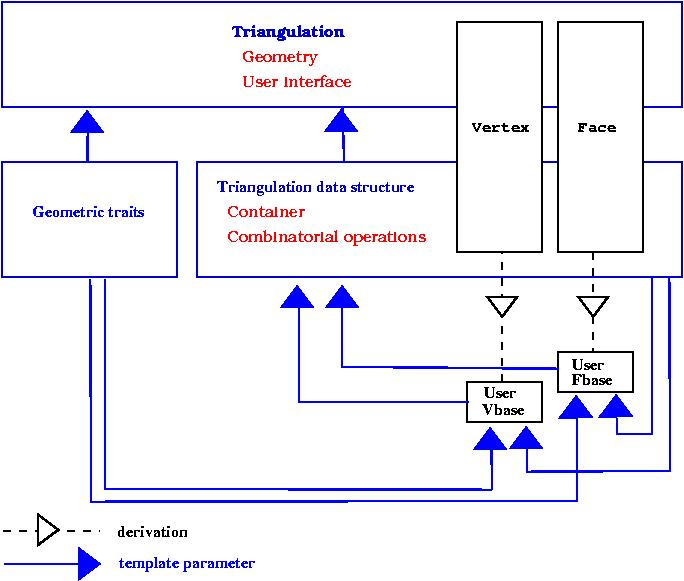
30.3.3   The Rebind Mechanism

The solution proposed by CGAL to resolve this cyclic dependency is based on a rebind mechanism similar to the mechanism used in the standard allocator class std::allocator. The vertex and face classes plugged in the instantiation of a triangulation data structure are themselves instantiated with a fake data structure. The triangulation data structure will then rebind these classes, plugging itself at the place of the fake data structure, before using them to derive the vertex and face classes. The rebinding is performed through a nested template class Rebind_TDS in the vertex and face class, which provide the rebound class as a type called Other.

Here is how it works schematically. First, here is the rebinding taking place in the triangulation data structure.

template < class Vb, class Fb >
class Triangulation_data_structure
{
  typedef Triangulation_data_structure<Vb,Fb>    Self;

  // Rebind the vertex and face base to the actual TDS (Self).
  typedef typename Vb::template Rebind_TDS<Self>::Other  VertexBase;
  typedef typename Fb::template Rebind_TDS<Self>::Other  FaceBase;

  // ... further internal machinery leads to the final public types:
public:
  typedef ...  Vertex;
  typedef ...  Face;
  typedef ...  Vertex_handle;
  typedef ...  Face_handle;
};

Then, here is the vertex class with its nested Rebind_TDS template class and its template parameter set by default to an an internal type faking a triangulation data structure.

template < class TDS = an internal type faking a triangulation data 
structure >
class Vertex_base
{
public:
  template < class TDS2 >
  struct Rebind_TDS {
    typedef Vertex_base<TDS2>    Other;
  };
...
};

typedef Triangulation_data_structure< Vertex_base<>, Face_base<> > TDS;

30.3.4   Making Use of the Flexibility

There is several possibilities to make use of the flexibility offered by the triangulation data structure.

• First, when the user needs to have, in vertices and faces, additional information which do not depend on types defined by the triangulated data structure, predefined classes Triangulation_vertex_base_with_info and Triangulation_face_base_with_info can be plugged in. Those classes have a template parameter Info to be instantiated by a user defined type. They store a data member of this type and gives access to it.
• Second, the user can derive his own base classes from the default base classes: Triangulation_ds_vertex_base_2, and Triangulation_ds_face_base_2 are the default base classes to be plugged in a triangulation data structure used alone. Triangulation classes requires a data structure in which other base classes have been plugged it. The default base classes for most of the triangulation classes are Triangulation_vertex_base_2, and Triangulation_face_base_2 are the default base classes to be used when the triangulation data structure is plugged in a triangulation class.

  When derivation is used, the rebind mechanism is slightly more involved, because it is necessary to rebind the base class itself. However the user will be able to use in his classes references to types provided by the triangulation data structure. For example,

  template < class Gt, class Vb = CGAL::Triangulation_vertex_base_2<Gt> >
  class My_vertex_base 
    : public  Vb
  {
  public :
    template < typename TDS2 >
    struct Rebind_TDS {
      typedef typename Vb::template Rebind_TDS<TDS2>::Other    Vb2;
      typedef My_vertex_base<Gt,Vb2>                           Other;
    };
  
    typedef typename Vb::Triangulation_data_structure    Tds;
    typedef typename Tds::Vertex_handle                  Vertex_handle;
    ......
  };
  

• At last the user can write his own base classes. If the triangulation data structure is used alone, the requirements for the base classes are described by the concepts TriangulationDSVertexBase_2 and TriangulationDSFaceBase_2. If the triangulation data structure is plugged into a triangulation class, the concepts for the vertex and base classes depends on the triangulation class. The most basic concepts, valid for basic and Delaunay triangulations are TriangulationVertexBase_2 and TriangulationFaceBase_2.

See section 29.11 for examples of using the triangulation data structure flexibility.